Deep Learning for Sleep Staging (2020.03)
Projects | | Links: Link1 | Link2
This algorithm instructs deep neural networks to primarily learn important EEG patterns for sleep staging. With a series of works, we demonstrated that our method obtained significant EEG features in the domain with improved classification performances.
We developed the robust and interpretable deep neural networks for sleep staging from EEG recordings.
Problem Definition
Although deep learning models have shown superior performances in several tasks compared to other algorithms, there remain some limitations: (1) neural networks often learn suboptimal representations, and (2) they are uninterpretable.
Inspired from recent works in clinical domains, which show that the features from the domain expertise could enhance the interpretability and robustness of the models, the objective of the project was to guide neural networks during the training phase to learn significant features, which are defined by domain knowledge. To be specific, we aimed to make neural networks for sleep staging to automatically extract important EEG patterns (e.g., alpha/delta/theta waves, sleep spindles, and k-complexes) for sleep staging and exploit those patterns during classification.
Approach
During sleep staging, technicians often look for specific EEG patterns. Here, the existences of some pattern are highly related to certain sleep stages: k-complexes, sleep spindles - N2 stages, delta waves - N3 stages. Furthermore, these EEG patterns are often defined by their morphological characteristics. For example, k-complexes can be defined by large-amplitude positive and negative peaks.
Our training methodology is a pre-training method where important EEG patterns are firstly being extracted, and the main training phase proceeds based on the extracted features. We introduced a convolutional neural network with a cosine similarity operator as its base operator to make the neural network selectively respond to important morphological shapes in EEG recordings. This convolutional neural network can be defined as follows: \[\begin{equation} o_{i}^{k} = \frac{\mathbf{w}^{k} \cdot \mathbf{x}_{[i;i+L-1]}}{\vert \mathbf{w}^{k} \vert \vert \mathbf{x}_{[i;i+L-1]} \vert}. \end{equation}\]
Furthermore, using the derivatives of cosine similarity, the derivative of error with regard to positions in convolutional filter weights can be written as: \[\begin{equation} \frac{\partial E}{\partial w_{i}^{k}} = \sum_{j}{\frac{\partial E}{\partial o_{j}^{k}}}\bigg( \frac{x_j}{\vert \mathbf{w}^{k} \vert \vert \mathbf{x}_{[j;j+L-1]} \vert} - \frac{w_{i}^{k}(\mathbf{w}^{k} \cdot \mathbf{x}_{[j;j+L-1]})}{\vert \mathbf{w}^{k} \vert^{3} \vert \mathbf{x}_{[j;j+L-1]} \vert} \bigg) \label{eq:backprop1}. \end{equation}\]
To simplify the calculation, the norms of each convolutional filter are normalized to one in our implementation. Thus, resulting forward and backward operation in cosine similarity convolution can be simplified as: \[\begin{equation} o_{i}^{k} = \frac{\mathbf{w}^{k} \cdot \mathbf{x}_{[i;i+L-1]}}{\vert \mathbf{x}_{[i;i+L-1]} \vert} \label{eq:approx_f} \end{equation}\]
Taking the derivative on the above equation, we get the following updates: \[\begin{equation} \frac{\partial E}{\partial w_{i}^{k}} = \sum_{j}{\frac{\partial E}{\partial o_{j}^{k}}}\frac{x_{i+j-1}}{\vert \mathbf{x}_{[j;j+L-1]} \vert} \label{eq:approx_b}. \end{equation}\]
We further attached one-max pooling architecture during the pre-training phase. In this way, neural networks can selectively learn from regions where important EEG patterns are located. With this architecture, derivatives are updated as follows: \[\begin{equation} \frac{\partial E}{\partial w_{i}^{k}} = \frac{\partial E}{\partial o_{j^{*}}^{k}}\frac{x_{i+j^{*}-1}}{\vert \mathbf{x}_{[j^{*};j^{*}+L-1]} \vert}. \end{equation}\]
In the above equation, gradient values will only reflect the waveform shapes of the significant segments regardless of amplitude changes in data. Thus, neural networks will better locate the template patterns in data and update their parameters from them.
Results
Performance improvement
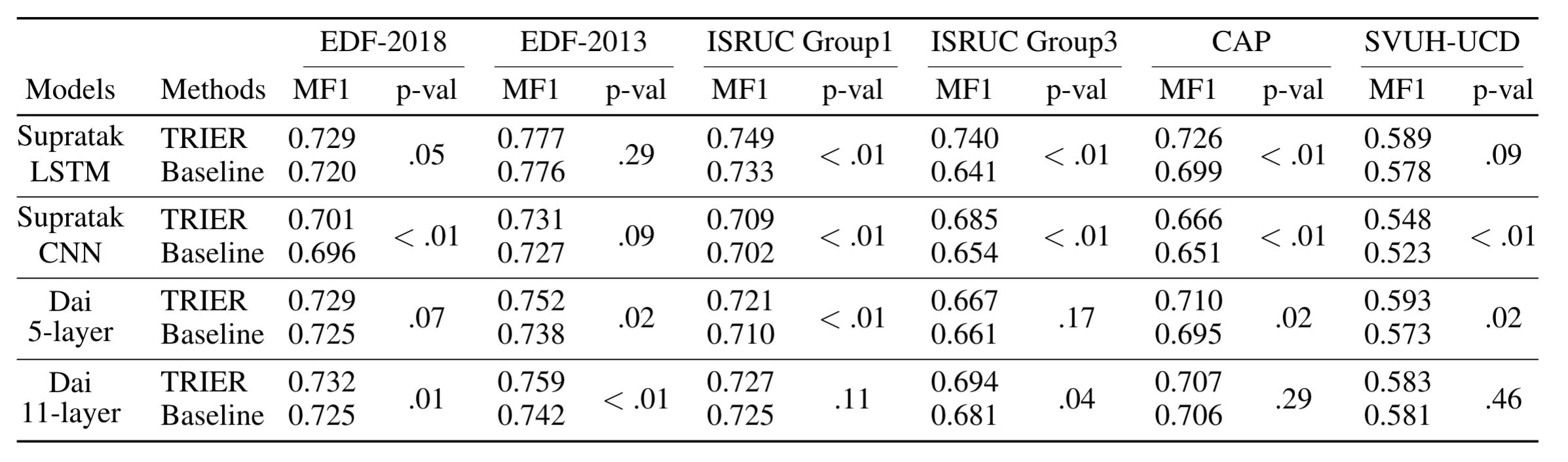
We validated our algorithm on several public EEG datasets. Compared to baseline neural networks, neural networks trained with our pre-training method achieved better sleep staging performances. Furthermore, improved performances for several neural network algorithms demonstrate that our pre-training method can be generally applied to sleep staging deep learning models. We attached some results from our paper.
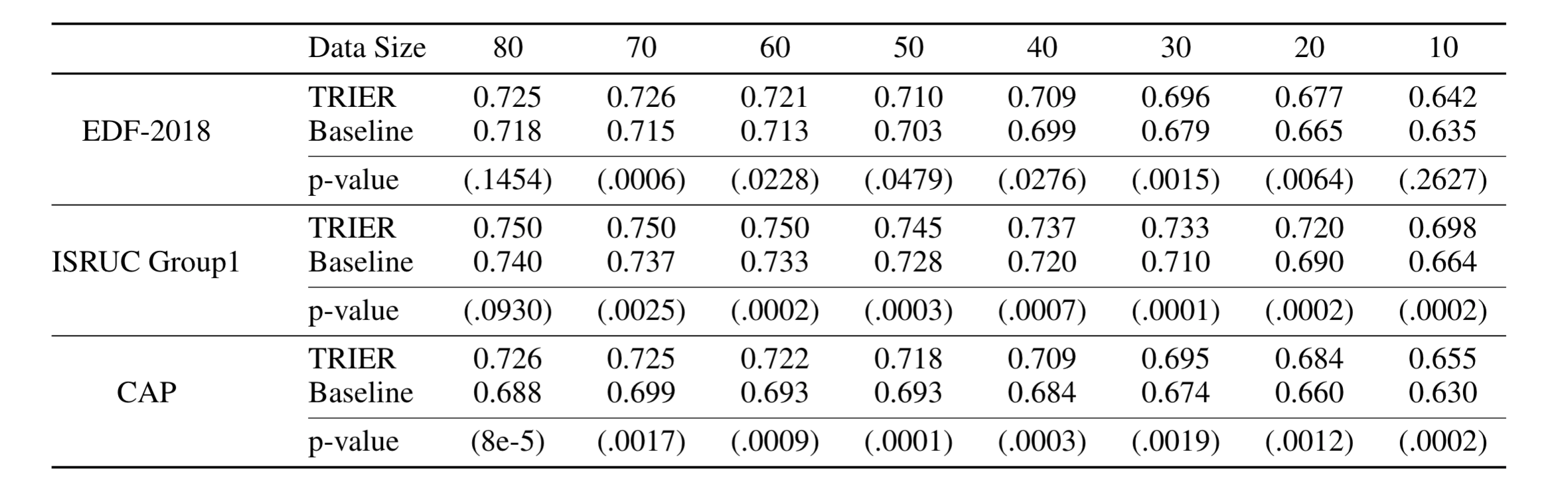
Performance from small training data
We also experimented with whether we can achieve superior performances when the training dataset is small. To do this, we deliberately reduced the size of the training dataset and trained the model on that dataset. After that, we evaluated the sleep staging performances on the test dataset. The following table shows the results.
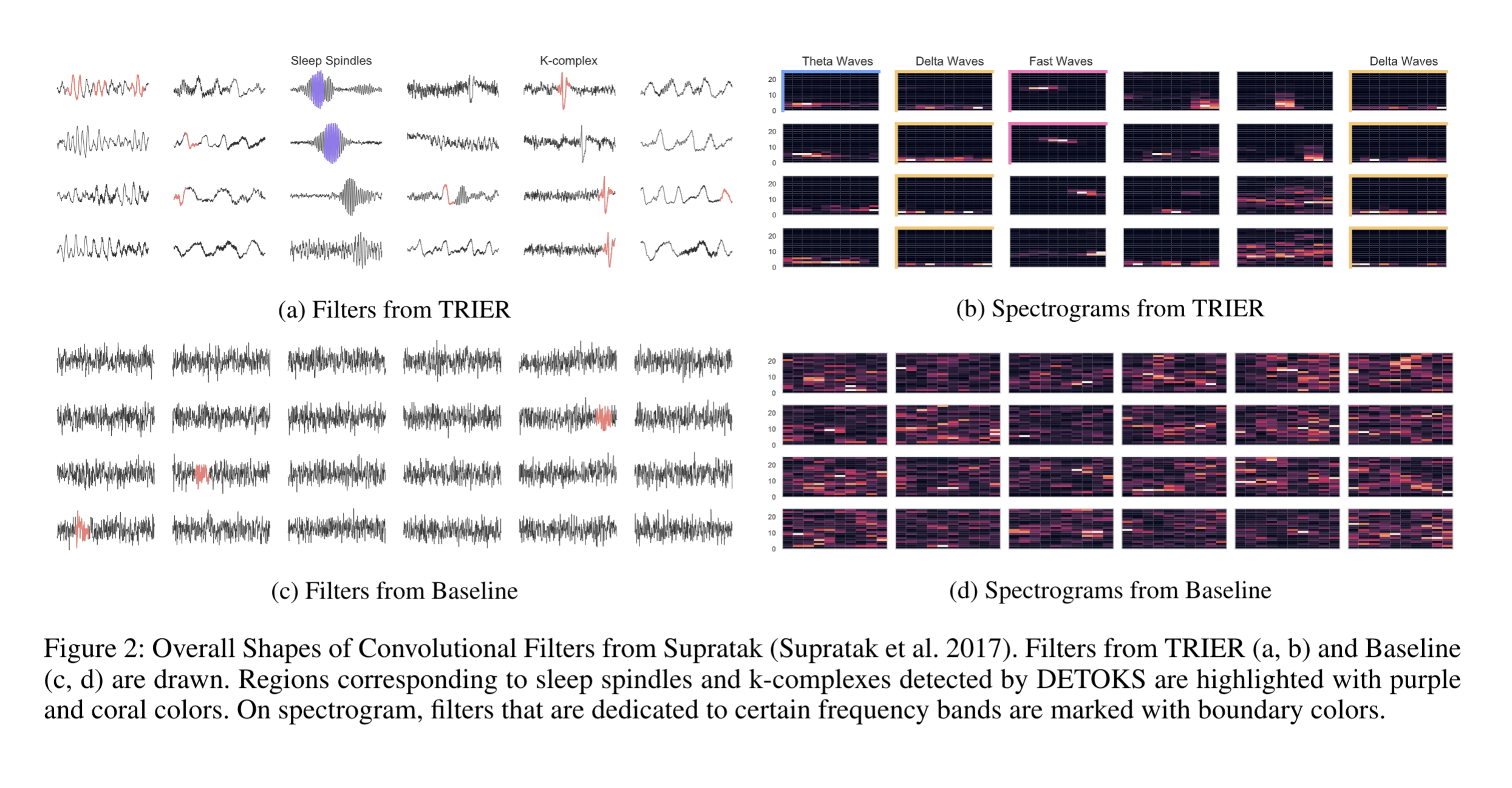
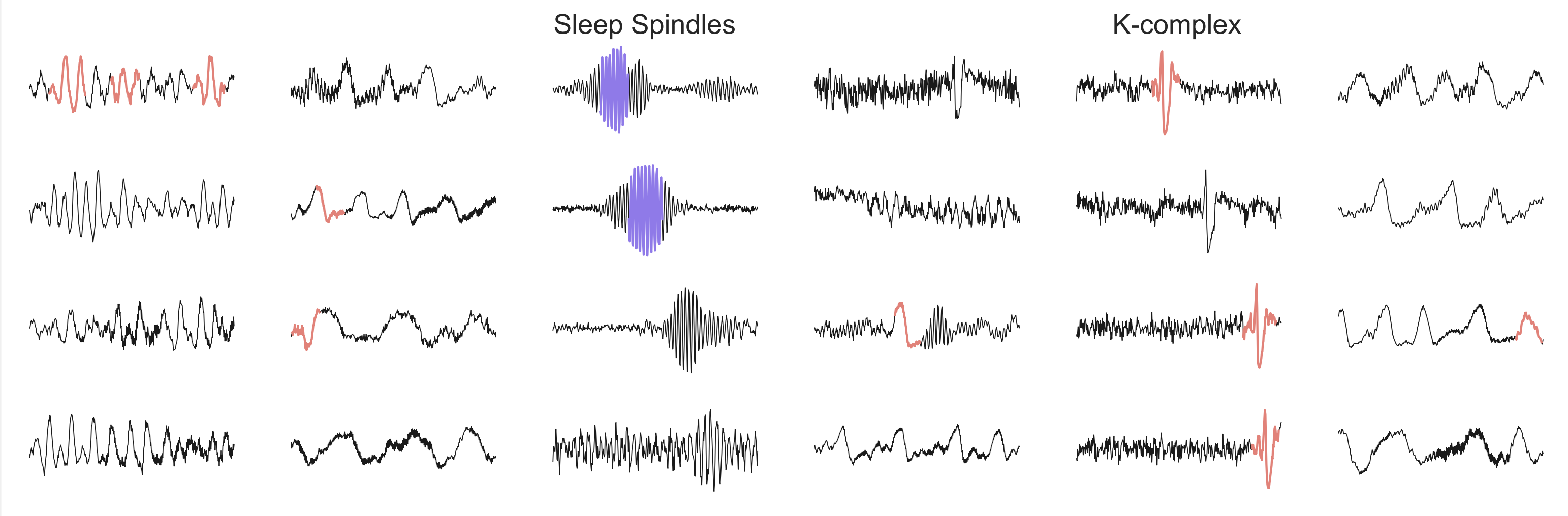
Learned features from the models
We further inspected the learned convolutional filters from the study. As seen in the figure below, our algorithm successfully extracted important EEG patterns for sleep staging. Without the deployment of external algorithms, our method automatically learned essential features in the clinical domain.
Publications
For further details on the project, please refer to the following papers published from the project.
- Lee, Taeheon*, Jeonghwan Hwang, and Honggu Lee. “Trier: Template-guided neural networks for robust and interpretable sleep stage identification from eeg recordings.” arXiv preprint arXiv:2009.05407 (2020).
- Lee, Taeheon*, Jeonghwan Hwang, and Honggu Lee. “Training Neural Networks with Domain Pattern-Aware Auxiliary Task for Sleep Staging.” ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2021.
(* indicates co-first author)
